How are sound levels measured?
Most people have heard of the unit called the decibel (dB), but not very many people understand how it works, or how to understand the values it describes.
In the simplest terms, the decibel measures the ratio between two signals. Notice that a ratio is being measured here! It is important to understand that the decibel does not measure a physical dimension such as mass, distance, or electrical current; rather, it measures the relative difference between two values of the same dimension.
The decibel is used for all kinds of scientific measurements where ratios are required; not just sound level, but also electrical or mechanical power and voltage to name but a few.
As was stated earlier, the human ear is sensitive to sounds that vary in volume by a factor of about 1 million. Whatever scale is used to measure volume, it must be capable of handling this huge dynamic range. Under these circumstances, it does not make sense to use a linear scale because it would have to run from 1 all the way up to 1 million—which would not be very practical. So what type of scale should be used to measure the level of a signal that varies over such a huge range?
A characteristic of human hearing very conveniently comes to our rescue. In order for you to perceive a doubling of the volume of a sound, the pressure level must in fact increase by a factor of 10. If you perceive a second doubling of sound volume, then the pressure level has gone up by a factor of 100 compared to the original sound.
This indicates that our ears are responding to increases in sound pressure in a logarithmic, not a linear manner. This now provides the answer for what scale should be used to measure the power and volume of sound. Since our ears respond logarithmically, it makes sense for our scale also to be logarithmic.
The decibel scale is just one example of a logarithmic scale. Other examples of logarithmic scales used in scientific measurement are the Richter scale for measuring the strength of earthquakes and the pH scale for measuring aciditiy or alkalinity. (The values used in pH scale are the negative log of the Hydrogen ion concentration—hence the name pH or “parts Hydrogen”)
Measuring the strength of a sound signal

Equation 3
We know that sound is the movement of energy through some medium—usually air. Therefore, if we measure the total amount of energy that passes through a particular point in a given time period, then we have a measure of the intensity of the sound.
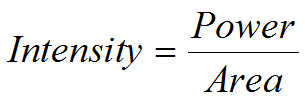
Equation 4
We also know that the amount of energy that passes a particular point in a given time period is a measure of power. Therefore, we can rewrite the above equation as follows:
So we can see that sound intensity is the amount of sound power per unit of area. Since power is measured in Watts and area in metres squared, the units of sound intensity are Watts per square metre (W/m2).
Comparing the power of two signals
Many experiments have been conducted on the sensitivity of human hearing, and it has been found that the smallest sound intensity that most people can hear is 0.000000000001 W/m2 or 1 x 10-12 W/m2. (Remember the anechoic chamber experiment?)
Let’s say that we’ve just taken some power measurements of two sounds and found one to have a value of 0.00079271 W/m2 and the other to have a value of 0.00000628 W/m2. We have already concluded that we should use a logarithmic scale to measure sounds, so let’s convert these values to their base 10 logarithms. (This effectively compresses the unwieldy decimal fractions down to manageable numbers containing far fewer digits.)
Log10(0.00079271) = -3.1
Log10(0.00000628) = -5.2
The Bel (named after Alexander Graham Bell) is the unit of power ratio. One tenth of a Bel, or a deciBel, represents a change in power that we can easily relate to in practice. Therefore, to quote the answers obtained from the previous calculations in decibels, we must multiply by 10.
-3.1 * 10 = -31
-5.2 * 10 = -52
If you remember your mathematics lessons, you will recall that two numbers can be multiplied by adding their logarithms, and divided by subtracting their logarithms. So to find out how many times louder one signal is compared to another, we would divide one into the other—or simply subtract their logarithms.
-31 - (-52) = 21dB
So the first signal is 21 dB louder than the second signal.
We now have a convenient way of comparing two unwieldy numbers. But this is still not quite useful enough for quoting the power of an audible sound. It is very important to understand the next point.
In order for a sound power ratio to be calculated, we must always compare two values. If we only have one power value, we cannot arrive at a power ratio unless we compare our measured value with some standard reference value. So the question is, “What value should be used as this reference?”
The answer is the value of the quietest sound a human can hear. This has been standardised at 1 x 10-12 Watts per square metre. Therefore, all values quoting the power ratio of an acoustic signal are always calculated with this minimum value as the reference point.
The sound power values used above can now be quoted as a decibel value relative to the quietest sound a human can hear.
10 * Log10(0.00079271/0.000000000001) = 89
10 * Log10(0.00000628/0.000000000001) = 68

Equation 5
So these two values still differ from each other by 21dB, but now the decibel values are quoted with reference to the quietest sound a human can hear.
In general, the formula for a power ratio in decibels is:
Where Isig is the intensity (power) of the signal being measured and Iref is the reference intensity (power) of 1 x 10-12 W/m2.
Measuring the pressure level of a sound signal
Up till now, we have only been talking about the power of a signal. Remember that power is a measure of the amount of energy passing a given point within a given time period. Unfortunately, this is does not give us measure of the volume of the sound as perceived by our ears. In technical terms, our perception of “volume” or “loudness” is measured as a sound pressure level (spl). After all, our ears can only hear something when vibrations in the air exert pressure upon the our eardrums.
Pressure is a measure of force per unit area. Force is measured in Newtons (N), so the units of pressure are Newtons per square metre (N/m2). The compound unit for pressure is Pascals (Pa).
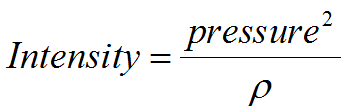
Equation 6
The most frequent use of a decibel value is to quote the ratio of sound pressure levels. Therefore, we must derive a method of quoting the spl in decibels. Fortunately, there is a direct relationship between sound intensity (I) and sound pressure (P).
Where ρ is the impedance of air (that’s the Greek letter rho by the way, not an italic letter p).
So what on earth is “Impedance”?
Impedance is a measure of how much the flow of a wave is resisted by the medium through which it is travelling. For air, this value is a real number (i.e. a number you can count to) and is determined by multiplying the speed of sound in air by the density of air.
However, the impedance of materials such as glass fibre insulation or Rockwool is a complex number (i.e. a number that has two parts—one you can count to called the “real part” and one you can’t count to called the “imaginary part”).
The impedance of air however varies with atmospheric pressure and temperature. For normal conditions at room temperature (1000 millibars pressure and 20°C), the value is roughly 400 (well OK, 413.47 to be exact, but 400 is close enough and makes the maths simpler).

Equation 7
So let’s rearrange equation 6 to be in terms of pressure:
Knowing that the intensity of the quiestest sound a person can hear is 1 x 10-12 W/m2, we can now calculate what this value is as a pressure:
0.00002 Pa = Sqrt(1 x 10-12 * 400)
At the other end of the scale is the threshold of pain, which has been given before as 1 Watt per square metre. This equates to a pressure of about 20 Pa.
20 Pa = Sqrt(1 * 400)
So, in terms of sound pressure levels, the range of human hearing is from 0.00002 Pa to 20 Pa.
So we’re done then with decibels?
Nope, not quite.
There’s one other thing to consider concerning the relationship between intensity and pressure. Notice that the intensity of a sound does not vary directly with pressure, but with the square of the pressure.
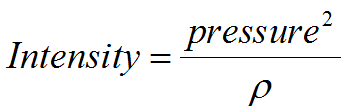
Equation 6

Equation 5
Here are equations 5 and 6 again. Notice in equation 6 that when the pressure doubles, the intensity will quadruple. When the pressure triples, the intensity goes up by a factor of nine. Also notice that we can replace intensity in equation 5, with “pressure squared over rho” (from equation 6) and then simplify:
dBspl = 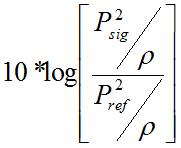 =
= 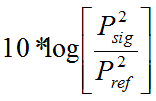 =
= 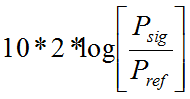 =
= 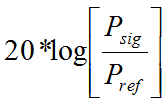

Equation 7
The only difference between the equation for SPL and the equation for power is that now we are multiplying 20 instead of 10. Where Psig is the sound pressure level of the sound being measured and Pref is the reference value of 0.00002 Pa.
99% of the time, a ratio of sound pressure levels is meant when you hear the term decibel. (This is the value displayed by a sound level meter). The problem is that almost nobody attaches the “spl” to the end of “dB”, which is not so much wrong, as just incomplete.
In the same way that the ratio of power measurements uses 1 x 10-12 W/m2 as its reference value, so the ratio of SPL measurements uses 0.00002 Pa as its reference value.