Wave basics
When we talk about sound, the word “wave” is frequently used. Webster’s dictionary (rather elaborately) defines a wave as:
“A disturbance or variation that transfers energy progressively from point to point in a medium and that may take the form of an elastic deformation or of a variation of pressure, electric or magnetic intensity, electric potential, or temperature.”
Which sound waves are we interested in?
There is a huge range of frequencies that can be described as “sound”. However, not all of these “sounds” can be detected by our biological microphones. In the case of audible sound, we are interested in the range of sound waves that occur between 20Hz and 20,000Hz. Above 20,000Hz is a range known as ultrasound (used extensively in medical research and examination), and below 20Hz is a range known as infrasound (an area of interest for seismologists).
So what does a wave traveling through air look like?

Figure 2: Longitudinal wave (Courtesy of Prof. Dan Russell)
Sound travels through air as a sequence of compression waves. The animation here shows how individual air “particles” move as a sound wave passes by. They bunch up to form an area of high pressure, then spread out to form an area of low pressure.
This is known as a “longitudinal” wave because the particles are moving backwards and forwards in the same direction as the wave is travelling.
One thing that is very important to realise here is that the individual air “particles” do not travel along with the wave. Instead, they simply move backwards and forwards as the wave passes by. Their overall net position does not change.
Wave properties
If we want to describe the physical properties of a wave, one of the first things to work out is how often the wave repeats its cycle — Once a week? Twenty times an hour? Four hundred times a second? Whatever number you come up with here is known as the wave’s “frequency”. It is usual to measure wave frequency in cycles per second — or to use the scientific unit, Hertz (abbreviated to Hz).
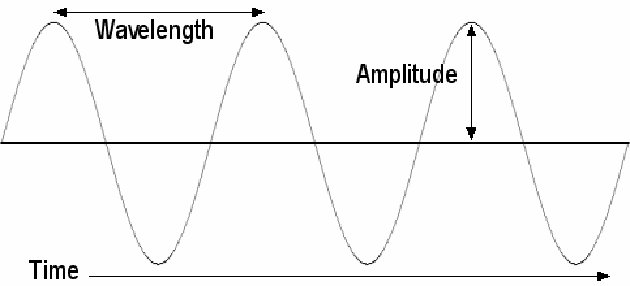
Figure 3: The properties of a wave
Now that we know how often a wave repeats its cycle, the next property to understand is what physical distance separates the same point in adjacent cycles. Another way of looking at this is to see how much space one cycle of the wave takes up. This is just a distance and is measured in metres. The length of one wave cycle is known (cunningly enough) as the wavelength.
For sounds audible to humans, the wavelength varies from 17.16m for a 20Hz signal, down to 17mm for a 20KHz signal.
Take another look at the animation. You will see that where air “particles” are bunched up together, this represents an area where the air pressure is slightly higher than the surrounding air pressure. Similarly, where the air “particles” are spread apart from each other, this represents an area where the air pressure is slightly lower. Using the animation as a simple example, if we were to plot a graph of how the air pressure rises and falls compared to the ambient air pressure, the graph would be a sine wave.
One last wave property that should be understood is the pressure difference between the maximum (or minimum) point in the wave cycle, and the ambient or average surrounding pressure. This is a measure of how much energy is being transmitted by the wave. The bigger the pressure difference, the more energy the wave carries. This property of a wave is known as the amplitude.
The energy of a sound wave is measured by a physicist as intensity, but perceived by our ears as loudness (remember that the physical quantity called “intensity” does not directly correspond with our perception of “loudness” or “volume”).
Fitting the pieces together
The simplest form of wave is known as a sine wave. If this wave form were to be played through an amplifier into a loudspeaker, you would hear a single, pure tone. A sine wave represents a sound of exactly one frequency.
In real life however, sounds are never as simple as pure tones. For instance, the sound of the human voice contains a huge number of different frequencies simultaneously. The specific combination of frequencies is what gives a person’s voice its characteristic sound.
We have seen that a sound wave has three basic properties: wavelength, frequency, and amplitude.
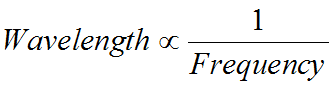
Equation 1: The inverse proportionality of wavelength and frequency
The wavelength and frequency of a wave are inversely proportional to each other. That means that as the wavelength increases, so the frequency decreases, and vice versa.
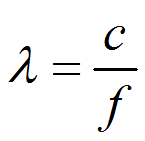
Equation 2
The constant of proportionality is the speed of sound (which varies depending on what medium the sound is travelling through).
In mathematical short hand, wavelength is denoted with the Greek letter lambda (λ), the speed of sound with the letter c, and frequency with f. So using this shorthand, the above proportionality can be rewritten as equation 2:
However, the speed of sound varies with air temperature and pressure. For almost all situations in architectural acoustics, the variation of the speed of sound caused by temperature changes can be ignored. The speed of sound in air at normal atmospheric pressure and 20°C is 343.25 m/s.
How is a sine wave formed?
One way a sine wave can be generated is by a simple harmonic oscillator (E.G. a weight bouncing up and down suspended by an ideal spring). Meanwhile back in reality, there is no such thing as an ideal spring, so a better real-life example would be the rise and fall of the piston in a car engine. If you were to plot the movement of the top of the piston against time, it would trace a sine wave.
This leads to a very important connection (no, not the crank shaft...)
There is a direct relationship between a sine wave and rotation. A piston rises and falls because it is attached to a rotating crank shaft, so it follows that there is a direct relationship between the angle through which the crank shaft has rotated and the position of the piston.
One complete revolution of the crank shaft produces one complete cycle of a sine wave. By choosing a particular starting point for the piston as a reference (say, top dead centre), we can determine how far through the sine wave cycle the piston has travelled.
Think of an engine containing two cylinders. When one piston is at the very top of its travel (top dead centre), the other piston will be at the very bottom of its travel (bottom dead centre). In order for these pistons to change places, the crank shaft must turn through half a rotation or 180°. If you draw the sine waves traced out by the two pistons on the same graph, you will see that they mirror each other's positions perfectly.
This difference of position is known as the phase relationship of the two waves.
Measuring the phase of a wave
Since there is a direct relationship between a sine wave and rotation, it makes sense to use the degrees of a circle to describe the position of a wave in its cycle. In physics, radians are used in preference to degrees, but both measure the same thing � an amount of rotation. There are 360° or 2π radians in a circle.
If two sine waves of equal frequency are perfectly aligned, then they are said to be “in phase”.
If two sine waves of equal frequency are one quarter of a wavelength out of phase, then they are said to be 90° (or π/2 radians) “out of phase”.
If two sine waves of equal frequency are 180° (or π radians) out of phase, then they are said to be “in anti-phase”.
What happens when two waves of the same frequency are played together?
The answer to this question depends on the phase relationship between the two waves. The effect of two waves being laid over top of each other is known as interference. This is most easily demonstrated with the following diagram.
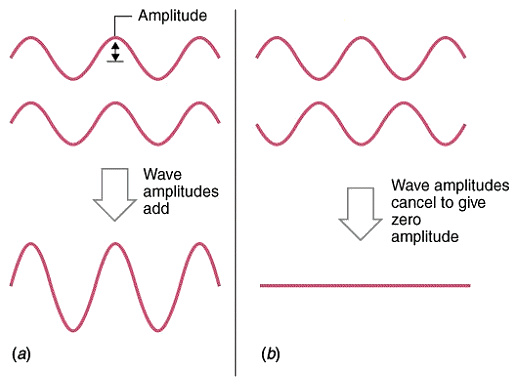
Figure 5: Constructive and destructive interference
On the left, the two waves rise and fall together � they are said to be “in phase”. Therefore, when their amplitudes are added, the result is another wave of the same frequency with double the amplitude.
This is called constructive interference.
On the right however, we see exactly the same two waves. But this time their alignment is such that when one wave is rising, the other is falling—they are said to be “in anti-phase”. Now when the amplitudes are added together, they cancel each other out and the result is zero or silence.
This is called destructive interference.
The concept of interference is very important when analysing the way sound (particularly down at the bass end) behaves in a room.
What happens when two waves of different frequency are played together?
Now, a slightly more complex situation occurs.
Since the frequency of these two waves is different, the phase relationship between them is continuously changing. Sometimes the waves are in phase and sometimes the waves are in anti-phase; but most of the time, they’re somewhere in between.
This means that there will be a continually varying degree of interference, ranging from constructive interference that makes the sound appear louder, to destructive interference that makes the sound appear quieter.
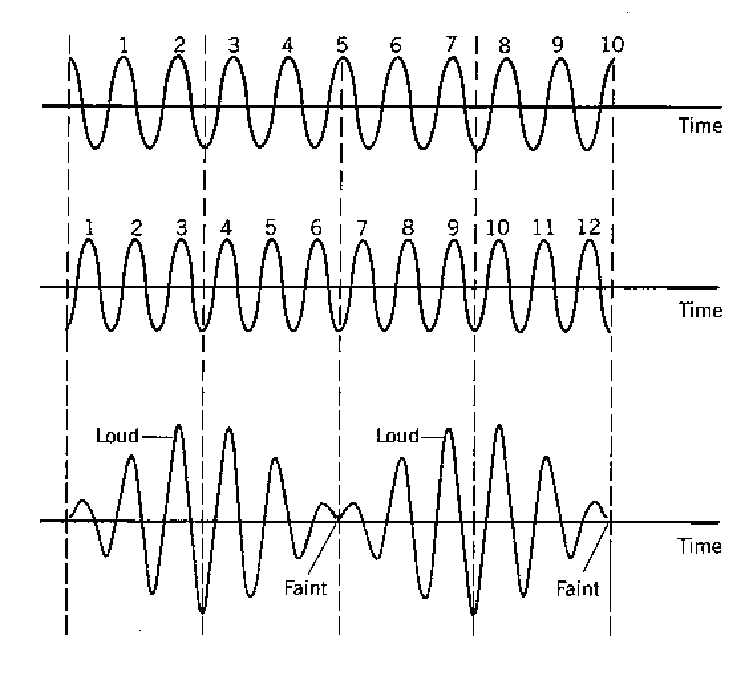
Figure 6: A beat frequency is formed when two waves of different frequencies interfere
The result is a fluctuating or pulsing effect is known as a “beat frequency”.
Listening to the beat frequency is a common trick used by piano tuners to see if the strings of one note are in tune with each other.
For the higher notes of a piano, the hammer actually hits three strings—and all three have to be perfectly tuned to each other.
Any tuning discrepancy between them will create a beat frequency which is a sure sign that the strings are not in tune.
The faster the beat frequency, the more out of tune the strings are.
As the beat frequency slows down, so the two strings come closer to each other in pitch. Eventually, the beat frequency will stop altogether, at which point the two string are perfectly in tune with each other.
